Aquí os paso el solucionario del tema 5 de Límites y Continuidad. (PINCHA)

Hola! Aquí os paso el diseño de la camiseta, en formato imagen (jpg) y formato pdf.

GRÁFICA DE FUNCIONES 4º ESO

En la red existen numerosos programas informáticos para representar funciones. Algunos software son de pago (con demos para probarlos durante un tiempo) y otros son libres siguiendo la filosofía 2.0. Rastreando la red he encontrado algunos interesantes para vuestro nivel. Destaco principalmente GRAPH 4.3, puedes descargarlo libremente pinchando  AQUÍ. Este programa tiene un entorno sencillo y las herremientas son bastante claras, nos permite representar funciones 'a trozos'. (Recordar que para elevar al cuadrado se coloca el simbolo ^). Este es el programa que he utilizado en la representación de la función 'a trozos' que hay en la anterior entrada del blog. Otra opción bastante asequible es usar la calculadora online WIRIS, que además de resolver ecuaciones, sistemas de ecuaciones... también representa gráficamente funciones. Espero que os sean herramientas útiles!

TRABAJO DE MATEMÁTICAS TEMA 12 (4º ESO)

4ºeso vacaciones 2ªeval

View more documents from Fran.

FUNCIONES A TROZOS 4º ESO (2)

Vamos a representar gráficamente la siguiente función definida a trozos:

Representemos primero las tres expresiones por separado como si fueran independientes y luego las consideraremos en común teniendo en cuenta los subdominios.

En primer lugar, g(x) = 5
Es una función contante que pasa por los puntos (x, 5) con xÎÂ (x ‘libre’ toma cualquier valor)
Su gráfica es:

En segundo lugar la función, h(x)=x²-6x+10
(para representarla es necesario calcular algunas cordenadas de la función cuadrática y calcular el vértice de la parábola) El vértice es (-b/2a, h(-b/2a)) Þ (3, h(3)) Þ (3, 1). Recuerda que el eje de simetría de la parábola es x = 3.
Gráficamente:

Por último la función: j(x) = 4x -15

Es una función afín creciente y para representarla basta con obtener dos coordenadas por donde para la función (que es una recta). Su gráfica es:

Y ya finalmente la función a trozos f(x), atendiendo a la información vista, queda del siguiente modo:

Ahora de la función a trozos podemos sacar información acerca de sus carcterísticas.

Dom f(x) = Â = (-µ, +µ)

Rec f(x) = [1, +µ)

f(x) en continua en  \ {2};      

La función corta al eje Y en el punto (0, 5).

Es una función constante en (-µ, 2], es decreciente en (2, 3) y creciente de (3, +µ). Presenta un mínimo relativo en x = 3.

FUNCIONES A TROZOS 4º ESO (1)

Una función definida a trozos es aquella que utiliza varias expresiones algebraicas para su definición, utilizando cada una de ellas en un determinado tramo del dominio de definición de la función principal.
Ejemplo:

Esa función es una parábola en el intervalo del eje X (-inf, 2). Y en el intervalo del eje X (2, +inf) es una función constante. Observar que hay una discontinuidad en el punto x = 2. Luego su Dom f(x) = |R - {2}.

Gráficamente:

MATEMÁTICAS 2º ESO. IES NIT DE L'ALBÀ

EJERCICIOS SOBRE T9: PROPORCIONALIDAD NUMÉRICA

1.- Calcula el valor del segmento que falta. Nombra los segmentos y las rectas.


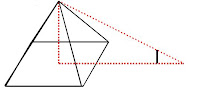
2.- La pirámide de Keops tiene una base cuadrada de 230 metros de lado. Dice la leyenda que Tales midió su altura observando que la sombra proyectada por la pirámide era de 85 metros desde la base y colocando su bastón de 1.46 m en el punto donde acaba la sombra, midió lo que proyectaba el bastón, que era de 2 m. ¿Qué altura tiene la pirámide?



3.- Los segmentos AB y CD miden 3 cm y 15 cm, y los segmentos EF y GH, 7 cm y 35 cm. Dibújalos y comprueba que son proporcionales.

4.- Un gran pino a las 11 de la mañana de un cierto día, arroja una sombra de 6,5 m. Próximo a él, una caseta de 2,8 m de altura proyecta una sombra de 70 cm. ¿Cuál es la altura del pino? Hacer un dibujo aproximado y explica qué tecnicas matemáticas has utilizado para resolver este problema.

5.- Justifica por qué los dos triángulos siguientes son semejantes. Calcula el resto de lados AB, B'C' y los ángulos que faltan.

6.- Calcula los valores de x e y aplicando el 'Teorema de Tales'.



7.- Sabiendo que la maqueta de la Torre Eiffel mide 15 cm y que su altura real de este monumento es 300 m, calcula:
a) La escala a la que está hecha la maqueta.

b) ¿A qué altura estará en la maqueta la segunda planta que, en realidad, se encuentra a 114 m del suelo?

TALLER DE MATEMÁTICAS 3º ESO, IES NIT DE L'ALBÀ

SISTEMAS DE ECUACIONES, 22 MARZO 2010

Realiza las siguientes actividades en un folio y al final de la clase entrégalo al profesor.

1.- Búsqueda en Internet: ¿Qué es una ecuación lineal con dos incógnitas? Pon varios ejemplos. También, ¿qué es un sistema de ecuaciones y para qué sirve? Pon varios ejemplos.

2.- Resuelve este sistema de ecuaciones con la calculadora WIRIS. Ver primero cómo resuelve wiris los sistemas de ecuaciones: Pincha AQUÍ

Calculadora Wiris

3.- Problemas: (Plantea cada uno de los problemas, resuélvelos con Wiris y comprueba que están bien)

a)En una granja hay conejos y patos. Si entre todos suman 18 cabezas y 52 patas, ¿cuántos conejos y patos hay?

b)Un hotel tiene habitaciones dobles (2 camas) y sencillas (1 cama). En total hay 50 habitaciones y 87 camas. ¿Cuántas habitaciones tiene de cada tipo?

c) En mi clase están 35 alumnos. Nos han regalado por nuestro buen comportamiento 2 bolígrafos a cada chica y un cuaderno a cada chico. Si en total han sido 55 regalos, ¿cuántos chicos y chicas están en mi clase?

d) El día del estreno de una película se vendieron 600 entradas y se recaudaron 196.250 ptas. Si los adultos pagaban 400 ptas. y los niños 150 ptas. ¿Cuál es el número de adultos y niños que acudieron?

TALLER DE MATEMÁTICAS 3º ESO - IES NIT DE L'ALBÀ
miércoles 3 febrero 2010
PRÁCTICA Nº 3: resolución de ecuaciones de 1er y 2º grado con wiris

Resuelve las siguientes actividades con la calculadora WIRIS:

a) 5(2 + 7x) - 10 = 34x
b) -2(1 - 3x) + 5 = 4(x + 2)
c) 5(2 + 3x) - (4 - x) = 4(1 + x) + 2
d) (x + 1)·(x - 3) + 3 = 0
e) 4x - (x² - 4) = 2x - 4


PROBLEMA:
Carmen tiene 42 años y su hijo 10. ¿Cuántos años tienen que pasar para que la edad de Carmen sea el triple que la del hijo?

Pincha AQUÍ para saber cómo resuelve WIRIS ecuaciones


ENLACES SOBRE ECUACIONES:
http://www.emathematics.net/es/ecuacion.php?a=3
http://www.araguez.net/mates/indicemate.htm
http://www.vadenumeros.es/tercero/ecuaciones-de-primer-grado.htm
http://es.wikipedia.org/wiki/Ecuaci%C3%B3n
www.oup.com/word/es/0330204003.doc
http://www.acienciasgalilei.com/mat/problemas/ejerc1mat-ecuaciones-1.htm